Now that you've started to build things that move, wouldn't it be cool if you could TALK about how they move?
I don't mean in the "Dude! My nifty robot just biffed into 50 pieces when it rolled off the table," sense. I mean in the NASA-type, "I'm going to tell you EXACTLY how it moved so you can build one too," sort of way. It might sometimes sound a little nerdy and stilted, but it is exactly this sort of precise language and careful description that enables us to land probes on other planets as well as design reliable and safe (and fast) cars, and so on. It might even help you on the occasional Physics test.
Most of this, all of you already know. You know how the "accelerator" speeds up a car and that the brake "decelerates" a car ("Deceleration" is the same as saying "acceleration in the opposite direction that you are moving.") You know that if you accelerate, you speed up (increase velocity) and if you decelerate, you slow down. Now we just need to get a little more precise about how we talk about it, how we use math to describe situations, and how we can use charts and graphs to really help understand what is going on.
There are two important aspects of accurately describing how things move: One is agreeing how we can all develop a common language to keep track of directions and measurements. The other is how to use the language and logic of mathematics to use what we have measured to make accurate predictions of how things will move in the future. Being able to speak about, and measure, and plot data surrounding motion is the first step.
So without worrying about the details, try fiddling with a couple if the simulations that I link to below. If you are even the slightest bit unsure or confused about how position, velocity, and acceleration are all interrelated and how each affects motion, or even how to use each of those terms to describe a situation, then these simulations are exactly what you need.
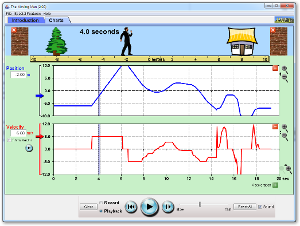
Move the Man. This is a neat little simulation where you can drag an icon of a person around and have it graph the position, velocity, and acceleration. Be sure to check the velocity and acceleration boxes at the bottom middle of the page under "Vectors" so you can see the
Using Hotwheels to learn about position, velocity and acceleration. This is a nice series of links that describe position, velocity, and acceleration. Be sure to click through all of the links on the left-hand side of the page to really understand the most typical situations, paying particular attention to the graphs of how each variable changes with respect to the others.
I don't mean in the "Dude! My nifty robot just biffed into 50 pieces when it rolled off the table," sense. I mean in the NASA-type, "I'm going to tell you EXACTLY how it moved so you can build one too," sort of way. It might sometimes sound a little nerdy and stilted, but it is exactly this sort of precise language and careful description that enables us to land probes on other planets as well as design reliable and safe (and fast) cars, and so on. It might even help you on the occasional Physics test.
Most of this, all of you already know. You know how the "accelerator" speeds up a car and that the brake "decelerates" a car ("Deceleration" is the same as saying "acceleration in the opposite direction that you are moving.") You know that if you accelerate, you speed up (increase velocity) and if you decelerate, you slow down. Now we just need to get a little more precise about how we talk about it, how we use math to describe situations, and how we can use charts and graphs to really help understand what is going on.
There are two important aspects of accurately describing how things move: One is agreeing how we can all develop a common language to keep track of directions and measurements. The other is how to use the language and logic of mathematics to use what we have measured to make accurate predictions of how things will move in the future. Being able to speak about, and measure, and plot data surrounding motion is the first step.
So without worrying about the details, try fiddling with a couple if the simulations that I link to below. If you are even the slightest bit unsure or confused about how position, velocity, and acceleration are all interrelated and how each affects motion, or even how to use each of those terms to describe a situation, then these simulations are exactly what you need.
The key thing to understand is how acceleration can be either aligned in the same direction with motion, in effect reinforcing it and speeding it (increasing its velocity), or acceleration can be aligned against motion, slowing the motion and decreasing the velocity.
In Physics we use the mathematical convention of sign (positive or negative numbers) to keep track of whether objects are accelerating in the same, or opposite direction they are moving. If an object is accelerating in the same direction it is moving, both the acceleration and velocity should have the same sign. If they are opposed, they have opposite signs.
Observe how the graphs reflect all of these. Learn how to look at something moving and make position, velocity and accelerations graphs, and learn how to look at these graphs and be able to describe how something is moving.
Also, observe how the relative DIRECTION of the acceleration versus the velocity has a big influence on motion. You'll be hearing more about vectors very soon.
Finally, do post questions or suggestions by clicking on the comments link below, and we will answer as soon as possible. (and note that you can post anonymously!)
